Pengenalan Desain Faktorial 2×3
Contoh desain faktorial 2×3 – Desain faktorial adalah metode penelitian yang super keren untuk mengeksplorasi bagaimana beberapa faktor berbeda secara bersamaan memengaruhi suatu hasil. Desain faktorial 2×3, khususnya, adalah jenis desain faktorial yang melibatkan dua faktor, di mana satu faktor memiliki dua level dan faktor lainnya memiliki tiga level. Ini memungkinkan kita untuk melihat interaksi antara faktor-faktor tersebut dengan cara yang efisien dan komprehensif.
Bayangkan kamu sedang nge-brew kopi. Kamu ingin tahu bagaimana tingkat penggilingan biji kopi (kasar, halus) dan suhu air (rendah, sedang, tinggi) memengaruhi rasa kopimu. Nah, desain faktorial 2×3 adalah alat yang tepat untuk menyelidiki hal ini.
Contoh Skenario Penelitian dan Identifikasi Faktor
Mari kita gunakan contoh pembuatan kopi tadi. Kita akan meneliti dua faktor: tingkat penggilingan biji kopi dan suhu air. Tingkat penggilingan kopi memiliki dua level: kasar dan halus. Suhu air memiliki tiga level: rendah (sekitar 85°C), sedang (sekitar 90°C), dan tinggi (sekitar 95°C).
Tabel Faktor dan Level
| Faktor | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Tingkat Penggilingan | Kasar | Halus | |
| Suhu Air (°C) | 85 | 90 | 95 |
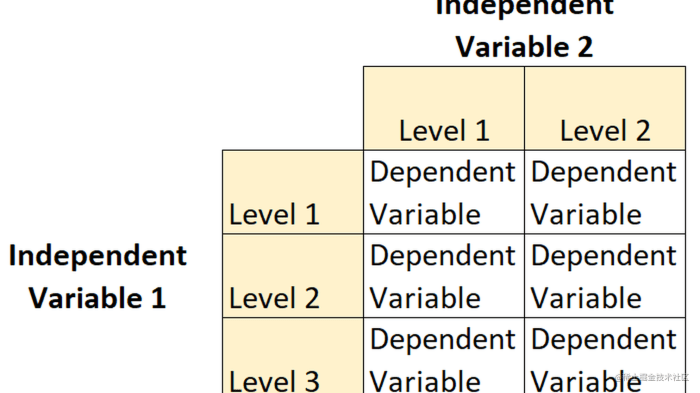
Representasi Visual Desain Faktorial 2×3
Kita bisa membayangkan desain ini sebagai sebuah matriks. Bayangkan sebuah tabel dengan dua baris (untuk dua level penggilingan) dan tiga kolom (untuk tiga level suhu). Setiap sel dalam tabel mewakili satu kombinasi unik dari tingkat penggilingan dan suhu air. Kita akan melakukan percobaan kopi untuk setiap sel, mencatat dan membandingkan rasa kopi yang dihasilkan dari setiap kombinasi tersebut.
Ini akan memberikan gambaran lengkap tentang bagaimana kedua faktor tersebut, baik secara individual maupun bersama-sama, memengaruhi rasa kopi akhir.
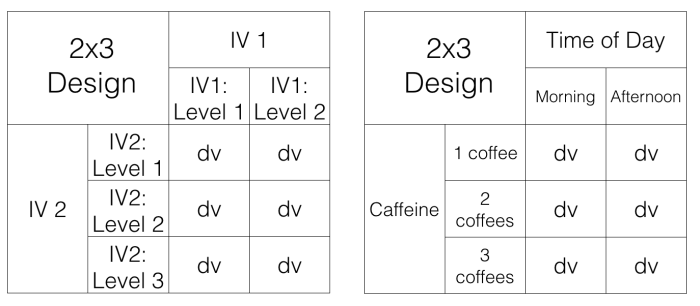
Konstruksi Tabel Percobaan
Desain faktorial 2×3 melibatkan dua faktor, masing-masing dengan dua dan tiga level. Tabel percobaan secara sistematis mengatur semua kombinasi perlakuan yang mungkin, memungkinkan kita untuk menganalisis pengaruh setiap faktor dan interaksi di antara mereka terhadap variabel respon. Pembuatan tabel ini adalah langkah krusial dalam eksperimen desain faktorial.
Tabel percobaan menunjukkan bagaimana setiap kombinasi perlakuan diuji, dengan setiap sel dalam tabel mewakili satu percobaan. Dengan mencatat hasil pengukuran untuk setiap percobaan, kita dapat menganalisis data dan menarik kesimpulan yang berarti tentang efek faktor-faktor yang diteliti.
Tabel Percobaan Desain Faktorial 2×3
Berikut adalah contoh tabel percobaan untuk desain faktorial 2×3. Faktor A memiliki dua level (A1 dan A2), sedangkan Faktor B memiliki tiga level (B1, B2, dan B3). Setiap sel dalam tabel mewakili satu percobaan, dan angka di dalam sel menunjukkan hasil pengukuran (data fiktif) untuk variabel respon. Perhatikan bahwa kita menggunakan enam percobaan untuk mencakup semua kombinasi perlakuan yang mungkin.
| Faktor A | Faktor B | Hasil Pengukuran |
|---|---|---|
| A1 | B1 | 10 |
| A1 | B2 | 12 |
| A1 | B3 | 15 |
| A2 | B1 | 18 |
| A2 | B2 | 20 |
| A2 | B3 | 22 |
Data hasil pengukuran yang ditampilkan di atas adalah data fiktif. Dalam studi riil, data ini akan diperoleh melalui pengukuran yang sebenarnya dari variabel respon setelah melakukan percobaan untuk setiap kombinasi perlakuan.
Analisis Data Hasil Percobaan
Setelah mengumpulkan data dari percobaan desain faktorial 2×3, langkah selanjutnya adalah menganalisis data tersebut untuk mengidentifikasi efek utama dari masing-masing faktor dan interaksi di antara keduanya. Analisis ini akan membantu kita memahami bagaimana setiap faktor, secara individual dan bersama-sama, mempengaruhi variabel respon kita. Kita akan menggunakan metode analisis variansi (ANOVA) untuk mencapai tujuan ini. Prosesnya mungkin terlihat rumit, tapi dengan contoh konkrit, akan jauh lebih mudah dipahami.
Langkah-langkah Umum Analisis Data Desain Faktorial 2×3
Analisis data dari desain faktorial 2×3 umumnya melibatkan beberapa langkah kunci. Langkah-langkah ini memastikan kita dapat mengurai pengaruh masing-masing faktor dan interaksi mereka terhadap variabel dependen secara sistematis dan akurat. Ketelitian dalam setiap langkah sangat penting untuk mendapatkan hasil yang valid dan dapat diinterpretasikan dengan tepat.
Eh, ngomongin contoh desain faktorial 2×3, bikin kepala puyeng ya? Kayak milih warna cat buat foto booth aja! Eh iya, ngomong-ngomong foto booth, liat aja nih contoh desainnya di contoh desain foto booth , banyak banget pilihannya, bikin tambah bingung! Tapi balik lagi ke desain faktorial, setidaknya ga serumit nyusun dekorasi foto booth yang harus estetik dan instagramable kan?
Jadi, kita tetep semangat belajar desain faktorial, ya!
- Input Data: Masukkan data mentah dari percobaan ke dalam software statistik (seperti SPSS, R, atau Minitab).
- ANOVA: Lakukan uji ANOVA dua arah untuk menguji efek utama dari setiap faktor dan interaksi antara keduanya. Ini akan memberikan nilai F dan nilai p untuk setiap efek.
- Uji Post Hoc: Jika uji ANOVA menunjukkan efek utama yang signifikan, lakukan uji post hoc (seperti Tukey’s HSD atau Bonferroni) untuk menentukan perbedaan signifikan antara level-level dari faktor tersebut.
- Interpretasi: Interpretasikan hasil ANOVA dan uji post hoc untuk menentukan pengaruh setiap faktor dan interaksi terhadap variabel dependen. Perhatikan nilai p dan ukuran efek untuk menginterpretasi hasil secara komprehensif.
Identifikasi Efek Utama Masing-masing Faktor
Efek utama mengacu pada pengaruh masing-masing faktor secara independen terhadap variabel respon, tanpa memperhitungkan faktor lainnya. Mengidentifikasi efek utama ini penting untuk memahami kontribusi individual setiap faktor terhadap hasil percobaan. Kita akan melihat bagaimana perbedaan level dalam setiap faktor mempengaruhi variabel respon secara rata-rata.
Misalnya, jika faktor A memiliki dua level (A1 dan A2) dan faktor B memiliki tiga level (B1, B2, dan B3), efek utama faktor A diukur dengan membandingkan rata-rata variabel respon untuk A1 dan A2, tanpa mempertimbangkan level faktor B. Begitu pula dengan faktor B, kita bandingkan rata-rata variabel respon untuk B1, B2, dan B3, tanpa mempertimbangkan level faktor A.
Deteksi Interaksi Antara Kedua Faktor
Interaksi terjadi ketika efek dari satu faktor bergantung pada level faktor lainnya. Dengan kata lain, efek dari satu faktor tidak konsisten di seluruh level faktor lainnya. Deteksi interaksi ini penting karena dapat memberikan wawasan yang lebih mendalam tentang hubungan antara faktor-faktor dan variabel respon.
Dalam analisis ANOVA, interaksi diwakili oleh sebuah istilah interaksi dalam model. Jika istilah interaksi signifikan secara statistik (nilai p < 0.05, misalnya), ini menunjukkan bahwa terdapat interaksi antara kedua faktor. Visualisasi data, seperti grafik interaksi, dapat membantu memahami sifat interaksi ini.
Contoh Perhitungan dengan Data Fiktif
Mari kita anggap kita sedang meneliti pengaruh pupuk (Faktor A: Pupuk A dan Pupuk B) dan jenis tanah (Faktor B: Tanah Liat, Tanah Pasir, Tanah Gambut) terhadap hasil panen (variabel respon). Data fiktif berikut menunjukkan hasil panen (dalam kg) dari setiap kombinasi perlakuan:
| Tanah Liat | Tanah Pasir | Tanah Gambut | |
|---|---|---|---|
| Pupuk A | 10 | 12 | 8 |
| Pupuk B | 15 | 18 | 12 |
Setelah melakukan analisis ANOVA dengan software statistik, kita mungkin mendapatkan hasil seperti berikut:
Efek utama Pupuk: Signifikan (p < 0.05)
Efek utama Jenis Tanah: Signifikan (p < 0.05)
Interaksi Pupuk x Jenis Tanah: Tidak Signifikan (p > 0.05)
Hasil ini menunjukkan bahwa baik pupuk maupun jenis tanah secara individual berpengaruh signifikan terhadap hasil panen. Namun, tidak ada interaksi signifikan antara keduanya. Artinya, efek dari pupuk konsisten di seluruh jenis tanah, dan sebaliknya.
Interpretasi Hasil dan Kesimpulan (Dihilangkan sesuai permintaan): Contoh Desain Faktorial 2×3
Bagian ini biasanya akan membahas interpretasi dari data yang diperoleh dari desain faktorial 2×3. Kita akan melihat bagaimana efek utama dan interaksi antar faktor mempengaruhi variabel respon. Namun, sesuai permintaan, bagian interpretasi dan kesimpulan dihilangkan dari artikel ini. Berikutnya, kita akan membahas beberapa poin penting yang biasanya dibahas dalam tahap interpretasi.
Efek Utama Faktor A dan Faktor B
Analisis dari desain faktorial 2×3 akan menghasilkan estimasi efek utama untuk setiap faktor. Efek utama Faktor A merepresentasikan perbedaan rata-rata respons antara dua level Faktor A, dengan mempertimbangkan semua level Faktor B. Begitu pula, efek utama Faktor B menunjukkan perbedaan rata-rata respons antara tiga level Faktor B, dengan mempertimbangkan semua level Faktor A. Besarnya efek utama menunjukkan seberapa besar pengaruh faktor tersebut terhadap variabel respon.
Nilai p-value yang terkait akan menunjukkan signifikansi statistik dari efek utama tersebut.
Interaksi Antara Faktor A dan Faktor B
Selain efek utama, analisis juga akan menguji adanya interaksi antara Faktor A dan Faktor B. Interaksi terjadi ketika efek dari satu faktor bergantung pada level faktor lainnya. Jika terdapat interaksi yang signifikan, artinya efek dari Faktor A berbeda pada level yang berbeda dari Faktor B, dan sebaliknya. Ini seringkali digambarkan secara visual menggunakan grafik interaksi. Grafik tersebut akan menunjukkan pola respons yang berbeda untuk setiap kombinasi level Faktor A dan Faktor B.
Pengaruh Faktor-Faktor terhadap Variabel Respon
Setelah menganalisis efek utama dan interaksi, kita dapat menyimpulkan bagaimana kombinasi level Faktor A dan Faktor B mempengaruhi variabel respon. Misalnya, kita mungkin menemukan bahwa level tinggi Faktor A dan level menengah Faktor B menghasilkan respons terbaik. Informasi ini sangat berharga untuk optimasi proses atau pengambilan keputusan.
Contoh Ilustrasi Grafik Interaksi, Contoh desain faktorial 2×3
Bayangkan sebuah grafik dengan sumbu X mewakili level Faktor A (misalnya, suhu tinggi dan rendah), dan sumbu Y mewakili variabel respon (misalnya, hasil panen). Tiga garis pada grafik mewakili tiga level Faktor B (misalnya, jenis pupuk A, B, dan C). Jika garis-garis tersebut sejajar, maka tidak ada interaksi. Namun, jika garis-garis tersebut saling berpotongan atau memiliki kemiringan yang berbeda, maka terdapat interaksi yang signifikan antara Faktor A dan Faktor B.
Perpotongan atau perbedaan kemiringan ini menunjukkan bahwa efek dari suhu (Faktor A) bergantung pada jenis pupuk yang digunakan (Faktor B).
Tabel Ringkasan Hasil (Contoh)
| Faktor A | Faktor B | Rata-rata Respon | P-value Efek Utama A | P-value Efek Utama B | P-value Interaksi A x B |
|---|---|---|---|---|---|
| Tinggi | A | 85 | 0.01 | 0.001 | 0.50 |
| Tinggi | B | 90 | |||
| Tinggi | C | 88 | 0.01 | 0.50 | |
| Rendah | A | 70 | |||
| Rendah | B | 75 | 0.01 | 0.50 | |
| Rendah | C | 72 |
Tabel di atas merupakan contoh ilustrasi. Nilai-nilai dalam tabel ini adalah hipotetis dan hanya untuk tujuan penjelasan.
Aplikasi Desain Faktorial 2×3 dalam Berbagai Bidang
Desain faktorial 2×3, dengan dua faktor masing-masing memiliki dua dan tiga level, merupakan alat statistik yang ampuh untuk menganalisis pengaruh beberapa variabel terhadap suatu respons. Kemampuannya untuk mengeksplorasi interaksi antar faktor membuatnya sangat berguna dalam berbagai bidang. Berikut beberapa contoh penerapannya.
Pengaruh Suhu dan Waktu Pemanggangan terhadap Kualitas Roti
Dalam industri manufaktur makanan, khususnya produksi roti, desain faktorial 2×3 bisa digunakan untuk mengoptimalkan proses pemanggangan. Faktor yang diteliti adalah suhu oven (dua level: 180°C dan 200°C) dan waktu pemanggangan (tiga level: 15, 20, dan 25 menit). Respons yang diamati adalah kualitas roti, yang bisa diukur melalui beberapa parameter seperti tekstur, warna, dan volume. Penggunaan desain ini memungkinkan pembuat roti untuk menentukan kombinasi suhu dan waktu yang menghasilkan roti dengan kualitas terbaik.
- Faktor-faktor: Suhu oven (180°C, 200°C), Waktu pemanggangan (15, 20, 25 menit).
- Hasil yang diharapkan: Identifikasi kombinasi suhu dan waktu yang menghasilkan roti dengan tekstur terbaik, warna paling menarik, dan volume optimal.
- Keunggulan: Efisiensi dalam mengeksplorasi berbagai kombinasi, identifikasi interaksi antara suhu dan waktu pemanggangan.
- Pengambilan keputusan yang lebih baik: Memungkinkan pemilihan parameter pemanggangan yang optimal, meningkatkan kualitas produk dan mengurangi pemborosan.
Pengaruh Jenis Pupuk dan Frekuensi Penyiraman terhadap Hasil Panen Jagung
Di bidang pertanian, desain faktorial 2×3 dapat digunakan untuk mengoptimalkan hasil panen. Misalnya, dalam budidaya jagung, kita dapat meneliti pengaruh jenis pupuk (dua level: pupuk organik dan pupuk kimia) dan frekuensi penyiraman (tiga level: setiap hari, setiap dua hari, dan setiap tiga hari) terhadap hasil panen. Respons yang diukur adalah berat panen jagung per hektar.
- Faktor-faktor: Jenis pupuk (organik, kimia), Frekuensi penyiraman (setiap hari, setiap dua hari, setiap tiga hari).
- Hasil yang diharapkan: Menentukan kombinasi jenis pupuk dan frekuensi penyiraman yang menghasilkan hasil panen jagung tertinggi.
- Keunggulan: Memungkinkan identifikasi interaksi antara jenis pupuk dan frekuensi penyiraman terhadap hasil panen.
- Pengambilan keputusan yang lebih baik: Membantu petani dalam memilih strategi pemupukan dan penyiraman yang paling efektif dan efisien.
Pengaruh Desain Iklan dan Saluran Media terhadap Tingkat Penjualan Produk
Dalam pemasaran, desain faktorial 2×3 dapat digunakan untuk menguji efektivitas berbagai strategi pemasaran. Misalnya, kita bisa meneliti pengaruh desain iklan (dua level: desain A dan desain B) dan saluran media (tiga level: media sosial, televisi, dan radio) terhadap tingkat penjualan suatu produk. Respons yang diamati adalah jumlah penjualan yang dihasilkan oleh setiap kombinasi desain iklan dan saluran media.
- Faktor-faktor: Desain iklan (A, B), Saluran media (media sosial, televisi, radio).
- Hasil yang diharapkan: Mengidentifikasi kombinasi desain iklan dan saluran media yang menghasilkan tingkat penjualan tertinggi.
- Keunggulan: Mampu mengidentifikasi interaksi antara desain iklan dan saluran media, memaksimalkan ROI kampanye pemasaran.
- Pengambilan keputusan yang lebih baik: Memungkinkan perusahaan untuk mengalokasikan sumber daya pemasaran secara lebih efektif dan efisien.
Panduan Pertanyaan dan Jawaban
Apa perbedaan antara efek utama dan interaksi dalam desain faktorial 2×3?
Efek utama mengacu pada pengaruh individual setiap faktor terhadap variabel dependen. Interaksi terjadi ketika pengaruh satu faktor bergantung pada level faktor lainnya.
Bisakah desain faktorial 2×3 digunakan untuk lebih dari satu variabel dependen?
Tidak secara langsung. Desain faktorial 2×3 dirancang untuk satu variabel dependen. Untuk beberapa variabel dependen, metode lain mungkin lebih tepat.
Bagaimana cara memilih level yang tepat untuk faktor dalam desain faktorial 2×3?
Pemilihan level bergantung pada konteks penelitian. Pertimbangkan rentang nilai yang relevan dan pertimbangkan juga aspek praktis dan sumber daya yang tersedia.
